自動車V&V開発プロセス:要件カスケーディング手法
HARDPOINTを用いた数値ベースアプローチ
目次
- はじめに
- V字モデルと検証プロセス
- HARDPOINTコンセプト – 重要な境界定義
- CAEベースの数値カスケーディング
- シーソーバランス手法
- ケーススタディ:NVH要件の分割
- 検証戦略
- ベストプラクティスと課題
- まとめ
1. はじめに
1.1 自動車業界におけるV&V開発プロセス
検証と妥当性確認(V&V:Verification and Validation)プロセスは、自動車開発の基盤であり、以下を保証します:
- 検証(Verification):仕様通りに製品が正しく作られているか
- 妥当性確認(Validation):顧客ニーズに合った正しい製品が作られているか
自動車のV字モデルにおいて、左側は検証(Verification)を表し、車両レベルの上位要件からサブシステム、コンポーネントレベルへと要件がカスケードされます。
1.2 要件カスケーディングの課題
自動車開発における最も重要な課題の一つは、車両レベルの上位要件をサブシステム要件へ適切に分割する方法です。これは特に以下の項目で重要です:
- NVH(騒音・振動・ハーシュネス)性能
- 衝突安全性能
- 燃費と排出ガス
- 乗り心地とハンドリング
本ドキュメントでは、CAEシミュレーションツールを用いた数値ベースのカスケーディング手法に焦点を当て、特にBody(車体)とPowerplant(パワープラント)の境界を定義するHARDPOINTコンセプトを重視します。
2. V字モデルと検証プロセス
2.1 V字モデル構造
上位レベル(車両)
│
├── 要件定義
│ └── 車両全体要件
│
├── システム設計
│ ├── ボディシステム要件
│ ├── パワープラントシステム要件
│ ├── シャシシステム要件
│ └── 電装システム要件
│
├── サブシステム設計
│ └── コンポーネント要件
│
└── コンポーネント設計
2.2 左側:検証プロセス
V字モデルの左側は要件の分割を表します:
- レベル1:車両レベル要件(例:「100km/h時の車内騒音 ≤ 65 dB(A)」)
- レベル2:システムレベル要件(例:ボディNVH、パワープラントNVH)
- レベル3:サブシステム要件(例:エンジンマウント仕様)
- レベル4:コンポーネント要件(例:マウントブッシュ剛性)
重要な問い:レベル1をレベル2へ科学的かつ数値的にどのように分割するか?
3. HARDPOINTコンセプト – 重要な境界定義
3.1 HARDPOINTとは何か?
HARDPOINT(ハードポイント)とは、2つの主要サブシステム間の物理的・機能的境界を定義する重要なインターフェース点です。ボディとパワープラントの分離においては:
HARDPOINT = パワープラントが車体に接続される取付点・マウント点
3.2 HARDPOINTの重要性
HARDPOINTが重要な理由:
- 明確な境界を責任と要件の観点から定義
- CAEとテストの両方で測定・検証ポイントとして機能
- ボディチームとパワープラントチームの独立した開発を可能にする
- 両チームが満たすべきインターフェース要件を提供
- 要件配分におけるシーソーの支点として機能
3.3 HARDPOINTの種類
自動車開発における一般的なHARDPOINT:
| サブシステムインターフェース | HARDPOINTの例 |
|---|---|
| ボディ-パワープラント | エンジンマウント、トランスミッションマウント、トルクロッドマウント |
| ボディ-サスペンション | サスペンション取付点、ショックタワー取付部 |
| ボディ-ステアリング | ステアリングコラム取付部、ラック取付部 |
| ボディ-排気系 | エキゾーストハンガー点 |
3.4 HARDPOINT要件定義
各HARDPOINTで以下のパラメータを定義する必要があります:
- 静的特性:位置(X, Y, Z)、剛性、荷重容量
- 動的特性:伝達率、インピーダンス、振動振幅
- 力・モーメント:6自由度すべての静的・動的荷重
- 変位:許容たわみ範囲
- 周波数応答:共振回避ゾーン
4. CAEベースの数値カスケーディング
4.1 CAEシミュレーションの役割
最新のCAE(Computer-Aided Engineering)ツールは、以下によりデータ駆動型の要件分割を可能にします:
- 車両全体挙動のシミュレーション
- サブシステム寄与度の解析
- HARDPOINT挙動の評価
- 要件配分の数値的根拠の提供
4.2 車両全体振動解析のためのCAEソフトウェア
RecurDynなどのマルチボディダイナミクス(MBD)ソフトウェアにより以下が可能:
- 車両全体の振動シミュレーション
- パワープラント動的解析(エンジン燃焼、アンバランス)
- 路面入力加振
- HARDPOINT力・変位解析
- 各サブシステムの寄与度解析
4.3 シミュレーションベースのカスケーディングプロセス
ステップ1: 上位要件の定義
↓
ステップ2: 車両全体CAEモデル構築(RecurDyn)
↓
ステップ3: 各種条件でシミュレーション実行
↓
ステップ4: HARDPOINT挙動の解析
↓
ステップ5: サブシステム寄与度の算出
↓
ステップ6: シーソーバランスを用いた要件配分
↓
ステップ7: マージンを含むサブシステム要件定義
4.4 CAEからの解析出力
RecurDynシミュレーションから以下を抽出:
- 車内騒音レベル(全体応答)
- ボディ固体伝播音の寄与(HARDPOINTから車内への経路)
- パワープラントの寄与(HARDPOINTでの音源)
- HARDPOINT力と変位(インターフェース挙動)
- 周波数応答関数(伝達関数)
5. シーソーバランス手法
5.1 シーソーコンセプト
要件分割はシーソーとして可視化できます:
車体NVH パワープラントNVH
(左側) (右側)
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\/
HARDPOINT
(支点/fulcrum)
← 車両全体NVH要件(バランス点)→
5.2 バランスの原則
車両全体のNVH性能は以下の組み合わせで決定されます:
- ボディ側寄与(固体伝播経路)
- パワープラント側寄与(加振源)
HARDPOINTにおいて:
- パワープラントからの入力:力、振動振幅
- ボディの応答:伝達率、騒音放射
重要な洞察:異なる組み合わせで同じ車両レベル性能を達成できます:
- 厳しいボディ要件 + 緩いパワープラント要件
- 緩いボディ要件 + 厳しいパワープラント要件
5.3 数学的表現
NVHについて、簡略化した関係式は次のように表現できます:
車内騒音 = f(パワープラント加振, HARDPOINTインターフェース, ボディ伝達率)
より具体的には:
L_interior = L_source + TL_hardpoint + TF_body
ここで:
- L_interior: 車内騒音レベル [dB]
- L_source: パワープラント音源レベル [dB]
- TL_hardpoint: HARDPOINTでの透過損失 [dB]
- TF_body: ボディ伝達関数 [dB]
または振動領域では:
a_interior = a_hardpoint × H_body
ここで:
- a_interior: 車内振動加速度
- a_hardpoint: HARDPOINT振動(パワープラントから)
- H_body: ボディ周波数応答関数
5.4 シーソーバランス戦略
戦略A:ボディ最適化アプローチ
- 厳しいボディ要件(低伝達率)
- より高いパワープラント加振を許容
- パワープラントが頻繁に変わる場合に有効(マルチバリアント)
戦略B:パワープラント最適化アプローチ
- 厳しいパワープラント要件(低加振)
- より高いボディ伝達率を許容
- ボディが複数モデルで流用される場合に有効
戦略C:バランスアプローチ
- 両方に適度な要件
- 実務で最も一般的
5.5 トレードオフの考慮事項
シーソーバランスを決定する際の考慮点:
| 要因 | ボディ側重視 | パワープラント側重視 |
|---|---|---|
| コスト | 高い(ボディダンピング、材料) | 高い(洗練されたエンジン、バランスシャフト) |
| 重量 | 重い(制振材) | 重い(バランス機構) |
| 柔軟性 | 複数パワープラントで流用可能 | 複数ボディで流用可能 |
| 開発時間 | 長い(複雑な構造) | 長い(洗練の反復) |
| 性能上限 | 質量制約で制限 | 燃焼基本原理で制限 |
6. ケーススタディ:NVH要件の分割
6.1 上位要件
要件ID: VEH-NVH-001 説明: アイドル時の車内騒音レベル 目標値: 運転席耳位置で ≤ 40 dB(A) 測定条件: エンジンアイドリング、全アクセサリOFF、ドア・窓閉
6.2 HARDPOINT定義:3点式エンジンマウントシステム
このケーススタディでは、典型的な3点式エンジンマウント構成を使用します:
6.2.1 マウント配置
車両前方
↑
[マウント#1 - 右前]
●
/ \
/ \
/ \
/ \
/ エンジン \
/ \
●--------------●
[マウント#2] [マウント#3]
左後方 右後方
(トルクロッド)
6.2.2 HARDPOINT仕様
| HARDPOINT | 位置 | 主要機能 | 剛性方向 |
|---|---|---|---|
| マウント#1 | 右前 | 上下支持、前後拘束 | Z軸(上下): 高<br>X軸(前後): 中<br>Y軸(左右): 低 |
| マウント#2 | 左後 | トルク反力、ロール拘束 | X軸: 高(トルクロッド)<br>Y軸: 中<br>Z軸: 中 |
| マウント#3 | 右後 | 上下支持、ピッチ拘束 | Z軸: 高<br>X軸: 中<br>Y軸: 中 |
6.2.3 HARDPOINT座標系
車両座標系:
- X軸: 前後方向(+ 前方)
- Y軸: 左右方向(+ 右方)
- Z軸: 上下方向(+ 上方)
エンジン座標系:
- クランクシャフト軸に整列
- 通常、車両座標系から傾斜
6.3 CAEシミュレーション設定(RecurDyn)
6.3.1 モデル構成要素
-
パワープラントアッセンブリ:
- エンジンブロック(質量特性を持つ剛体)
- クランクシャフト(アンバランスを持つ回転部品)
- トランスミッション(フレキシブルカップリング経由で接続)
- 補機類(オルタネータ、A/Cコンプレッサー)
-
3点マウントシステム:
- マウント#1, #2, #3(6自由度剛性・減衰を持つブッシュ要素)
- 現実的な非線形特性
-
車体:
- フレキシブルボディ(FEAからのモーダル表現)
- フロアパネル、ダッシュパネル、ピラー構造
- 車内空間(音響ボリューム)
-
加振源:
- エンジン点火周波数:4気筒4サイクル = 2次成分(2 × RPM/60)
- アイドル時:800 RPM → 26.7 Hz主要加振
- クランクシャフトに作用する燃焼力
- エンジンアンバランス力
6.3.2 シミュレーションケース
| ケース | RPM | 負荷 | 目的 |
|---|---|---|---|
| ケース1 | 800 | アイドル | 主要解析ケース |
| ケース2 | 1500 | 部分負荷 | 感度チェック |
| ケース3 | 3000 | 全負荷 | 広範囲妥当性確認 |
6.4 CAE解析結果
6.4.1 車両全体応答
シミュレーション結果: 運転席耳位置での車内騒音 = 42.5 dB(A)(ベースライン設計)
これは目標値40 dB(A)を2.5 dB超過しており、改善が必要です。
6.4.2 HARDPOINT力解析
アイドル時(800 RPM)の各HARDPOINT測定力:
| HARDPOINT | 周波数 | Fx [N] | Fy [N] | Fz [N] | 支配的成分 |
|---|---|---|---|---|---|
| マウント#1 | 26.7 Hz | 15.2 | 8.3 | 45.6 | 上下方向(2次成分) |
| マウント#2 | 26.7 Hz | 68.5 | 12.1 | 22.3 | 前後方向(トルク反力) |
| マウント#3 | 26.7 Hz | 12.8 | 6.7 | 38.2 | 上下方向(2次成分) |
観察:
- マウント#1と#3では上下方向力が支配的(点火周波数)
- マウント#2では前後方向力が支配的(トルクロッド反力)
6.4.3 寄与度解析
RecurDynの寄与度解析機能を使用:
車内騒音合計: 42.5 dB(A)
│
├── パワープラント寄与: 38.2 dB(A)
│ ├── エンジン2次成分: 36.8 dB(A)
│ ├── エンジン4次成分: 28.5 dB(A)
│ └── その他高調波: 25.3 dB(A)
│
└── ボディ増幅係数: +4.3 dB
├── フロアパネル共振: +3.8 dB
├── ダッシュパネル共振: +2.1 dB
└── 音響空洞モード: +1.5 dB
重要な発見:
- パワープラントはHARDPOINTで38.2 dB(A)を発生
- ボディ構造がこれを4.3 dB増幅し、運転席耳位置で42.5 dB(A)に到達
6.4.4 伝達関数解析
HARDPOINTから車内へのボディ伝達関数:
H_body = 車内応答 / HARDPOINT入力
26.7 Hz(アイドル点火周波数)において:
- マウント#1 → 運転席耳: 1.65(4.35 dB増幅)
- マウント#2 → 運転席耳: 0.98(-0.17 dB減衰)
- マウント#3 → 運転席耳: 1.52(3.64 dB増幅)
加重平均: 1.64(4.3 dB増幅)
6.5 シーソーバランス配分
6.5.1 現状分析
目標値: 40.0 dB(A) ← HARDPOINT → 現状: 42.5 dB(A)
●
改善必要量: -2.5 dB
車内騒音を2.5 dB低減する必要があります。これは以下により達成可能:
- 選択肢A: パワープラント加振を低減
- 選択肢B: ボディ増幅を低減
- 選択肢C: 両方の組み合わせ
6.5.2 配分オプション
選択肢A:パワープラント重視(70/30分割)
- パワープラント低減: -1.8 dB(38.2から36.4 dB(A)へ at HARDPOINT)
- ボディ改善: -0.7 dB(+4.3から+3.6 dB増幅へ)
選択肢B:ボディ重視(30/70分割)
- パワープラント低減: -0.8 dB(38.2から37.4 dB(A)へ at HARDPOINT)
- ボディ改善: -1.7 dB(+4.3から+2.6 dB増幅へ)
選択肢C:バランス(50/50分割)
- パワープラント低減: -1.25 dB(38.2から36.95 dB(A)へ at HARDPOINT)
- ボディ改善: -1.25 dB(+4.3から+3.05 dB増幅へ)
6.5.3 選択した戦略:選択肢C(バランス)
コスト、実現可能性、開発時間を考慮し、選択肢Cを選択します。
6.5.4 サブシステム要件定義
サブシステム要件:パワープラントNVH
| 要件ID | 説明 | 目標値 | 測定点 | 条件 |
|---|---|---|---|---|
| PP-NVH-001 | エンジンマウント力 – マウント#1(Z軸) | ≤ 38.5 N | HARDPOINT #1 | アイドル、800 RPM |
| PP-NVH-002 | エンジンマウント力 – マウント#2(X軸) | ≤ 58.0 N | HARDPOINT #2 | アイドル、800 RPM |
| PP-NVH-003 | エンジンマウント力 – マウント#3(Z軸) | ≤ 32.3 N | HARDPOINT #3 | アイドル、800 RPM |
| PP-NVH-004 | HARDPOINT振動レベル(加重) | ≤ 36.95 dB(A) | 全HARDPOINT | アイドル、800 RPM |
サブシステム要件:ボディNVH
| 要件ID | 説明 | 目標値 | 測定点 | 条件 |
|---|---|---|---|---|
| BD-NVH-001 | 伝達関数 – マウント#1→運転席 | ≤ 1.45(3.2 dB) | HARDPOINT #1 → 車内 | 20-30 Hz範囲 |
| BD-NVH-002 | フロアパネル1次曲げモード | > 35 Hz | フロア中央 | モーダル解析 |
| BD-NVH-003 | ダッシュパネル伝達率 | ≤ 1.2(1.6 dB) | ダッシュ中央 → 車内 | 20-30 Hz範囲 |
| BD-NVH-004 | 全体増幅係数 | ≤ +3.05 dB | HARDPOINT → 車内 | アイドル周波数 |
6.5.5 HARDPOINTでのインターフェース要件
ボディチームとパワープラントチームの両方が満たすべきインターフェース要件:
| インターフェース要件ID | 説明 | 目標値 | 責任 |
|---|---|---|---|
| IF-NVH-001 | マウント#1静的剛性(Z軸) | 350 ± 50 N/mm | パワープラント(マウント設計) |
| IF-NVH-002 | マウント#1動的剛性比 | 1.8 – 2.2 | パワープラント(マウント設計) |
| IF-NVH-003 | ボディ側ブラケット剛性(マウント#1) | > 10,000 N/mm | ボディ(ブラケット設計) |
| IF-NVH-004 | HARDPOINT位置公差 | ± 3 mm(X, Y, Z) | 両方(調整) |
| IF-NVH-005 | マウント取付トルク | 45 ± 5 Nm | 組立プロセス |
6.6 配分要件に基づく設計改善
6.6.1 パワープラント側アクション
HARDPOINTで36.95 dB(A)を達成するため(38.2 dB(A)から1.25 dB低減):
-
バランスシャフト追加
- 2次成分力をキャンセルする副軸バランスシャフトを追加
- 予想低減量: -0.8 dB
-
エンジンマウント最適化
- マウント#1上下剛性を低減: 400 → 350 N/mm
- トルク反力向上のためマウント#2の向きを調整
- 予想低減量: -0.3 dB
-
クランクシャフトバランシング
- バランス公差をグレード2.5からグレード1.0に改善
- 予想低減量: -0.15 dB
合計予想: -1.25 dB ✓
6.6.2 ボディ側アクション
増幅を+4.3 dBから+3.05 dBに低減(1.25 dB低減)するため:
-
フロアパネル剛性向上
- 補強リブを追加し1次曲げモードを上昇: 28 Hz → 36 Hz
- 予想低減量: -0.6 dB
-
ダッシュパネルダンピング
- 高応力エリアに制振材(ビチューメンシート)を適用
- 予想低減量: -0.4 dB
-
マウントブラケット最適化
- ブラケット剛性を向上し局所変形を低減
- 予想低減量: -0.25 dB
合計予想: -1.25 dB ✓
6.7 CAEによる検証
CAEモデルに改善を実装後:
更新されたRecurDynシミュレーション結果:
- HARDPOINTでのパワープラント加振: 37.1 dB(A)(目標: 36.95、マージン: +0.15)
- ボディ増幅: +2.9 dB(目標: +3.05、マージン: 0.15)
- 最終車内騒音: 40.0 dB(A) ✓(目標値を正確に達成)
7. 検証戦略
7.1 カスケードされた要件のV&Vプロセス
検証レベル テスト・解析方法
─────────────────────────────────────────────
コンポーネントレベル
├── マウントブッシュ試験 → 材料特性評価
├── ブラケット剛性 → 静的荷重試験
└── モーダル試験 → インパクトハンマー試験
サブシステムレベル
├── パワープラント試験台 → 加振台、ランアップ試験
│ 測定: HARDPOINT力
│
└── ボディ構造試験 → 音響加振
測定: 伝達関数
システムレベル
├── 車両プロトタイプ → 半無響室
└── HARDPOINT妥当性確認 → 力・加速度センサー
車両レベル
└── 最終妥当性確認 → 顧客走行条件
測定: 車内騒音
7.2 HARDPOINT検証
HARDPOINTでの重要な検証:
CAE-テスト相関:
- 各HARDPOINTに3軸力トランスデューサを設置
- 両側(パワープラントとボディ)に加速度計を設置
- エンジンランアップ中に測定(800 – 3000 RPM)
- RecurDyn予測と比較
- 目標相関: 力の大きさ±10%以内、位相±5°以内
合格基準:
- HARDPOINT力が配分された限界値内
- パワープラントチームとボディチーム両方の試験が独立して合格
- 統合試験で車両レベル目標を確認
7.3 トレーサビリティマトリクス
| 車両要件 | システム要件 | HARDPOINTインターフェース | 検証方法 |
|---|---|---|---|
| VEH-NVH-001<br>車内 ≤40 dB(A) | PP-NVH-004<br>HARDPOINT ≤36.95 dB(A) | IF-NVH-001~005<br>マウント剛性、位置 | パワープラント試験台<br>力トランスデューサ |
| VEH-NVH-001<br>車内 ≤40 dB(A) | BD-NVH-004<br>増幅 ≤+3.05 dB | IF-NVH-003<br>ブラケット剛性 | ボディ音響試験<br>加振台加振 |
| VEH-NVH-001<br>車内 ≤40 dB(A) | 組合せ | 組合せ | 車両プロトタイプ<br>半無響室試験 |
7.4 試験シーケンス
-
フェーズ1:コンポーネント検証(1-2週目)
- マウント剛性特性評価
- 材料減衰測定
-
フェーズ2:サブシステム検証(3-5週目)
- 試験台上のパワープラント(HARDPOINT力)
- ボディ構造音響試験(伝達関数)
-
フェーズ3:統合検証(6-8週目)
- パワープラントのボディへの組付
- HARDPOINT相関チェック
- 初期車両試験
-
フェーズ4:車両妥当性確認(9-12週目)
- 室内での車両全体試験
- 実路妥当性確認
- 顧客評価
8. ベストプラクティスと課題
8.1 ベストプラクティス
8.1.1 HARDPOINT定義
✓ 開発プロセスの早期にHARDPOINTを定義 ✓ 物理的な取付点をHARDPOINTとして使用(測定可能) ✓ HARDPOINT座標系を正確に文書化 ✓ HARDPOINT仕様に公差を含める
8.1.2 CAEシミュレーション
✓ 過去の車両データでCAEモデルを妥当性確認 ✓ チーム間で一貫したモデリング手法を使用 ✓ 非線形効果を含める(マウント剛性、接触) ✓ ロバスト性を理解するため感度解析を実施
8.1.3 要件配分
✓ 安全マージンを含める(NVHでは通常10-20%) ✓ 配分時に製造ばらつきを考慮 ✓ シーソー配分でコストと性能をバランス ✓ プラットフォーム戦略と整合(ボディ/パワープラント流用)
8.1.4 組織
✓ HARDPOINT要件の明確な所有権(両側) ✓ ボディとパワープラントチーム間の定期的インターフェース会議 ✓ HARDPOINT特性の共有CAEデータベース ✓ 開始時からの共同検証計画
8.2 よくある課題
8.2.1 課題:あいまいなHARDPOINT定義
問題: チーム間で境界の位置について意見が合わない 解決策:
- ボルト中心線をHARDPOINT基準として使用
- 測定面を明確に定義(ボディ側またはマウント側)
- 図面付きのインターフェース管理文書(ICD)を作成
8.2.2 課題:CAEモデル相関
問題: CAE予測が試験結果と一致しない 解決策:
- 過去の車両から相関データベースを構築
- まずHARDPOINT相関に焦点(局所精度)
- 試験測定モーダルパラメータでFEモデルを更新
- 正確なボディ表現のためRecurDynのフレキシブルボディ機能を使用
8.2.3 課題:過剰制約要件
問題: 配分後、両サブシステムが目標を達成できない 解決策:
- シーソーバランスを見直す(配分をシフト)
- 上位要件の実現可能性を検討
- 技術アップグレードを考慮(アクティブマウント、チューンドアブソーバー)
- マージン戦略を再評価
8.2.4 課題:後期設計変更
問題: 一方のサブシステムが設計変更し、HARDPOINTに影響 解決策:
- 影響評価付きの変更管理プロセスを確立
- 承認前にCAE再シミュレーションを要求
- 対応のためのインターフェースマージンを維持
- 可能な限りモジュラー設計を使用
8.2.5 課題:マルチフィジックス連成
問題: NVH改善が他の属性(耐久性、衝突)を悪化させる 解決策:
- HARDPOINTでの多目的最適化
- CAEに全属性を含める(RecurDyn + LS-DYNA + 疲労)
- システムエンジニアリングとのトレードオフ解析
- パレートフロンティア探索
8.3 高度なトピック
8.3.1 周波数依存配分
異なる加振周波数では、シーソーバランスが変化する可能性:
- アイドル(26.7 Hz): バランス配分
- 巡航(60 Hz): ボディ重視(構造共振)
- 加速(広帯域): パワープラント重視(過渡加振)
8.3.2 多属性HARDPOINT
HARDPOINTは複数の要件を満たす必要:
- NVH(低動的力)
- 耐久性(疲労寿命)
- 衝突(エネルギー吸収、侵入)
- パッケージング(空間制約)
解決策: 優先順位付けによる加重最適化
8.3.3 HARDPOINTでのアクティブシステム
新興技術:
- アクティブエンジンマウント(低周波振動をキャンセル)
- セミアクティブマウント(適応剛性)
- 更新された配分手法が必要(制御権限)
9. まとめ
9.1 重要なポイント
-
HARDPOINTは要件カスケーディングの支点
- ボディとパワープラントの境界を明確に定義
- インターフェース制御を伴う独立した開発を可能にする
- 測定可能な検証ポイントを提供
-
CAEシミュレーション(RecurDyn)により数値配分が可能
- 車両全体解析が寄与度データを提供
- 主観的判断を物理ベース配分に置き換える
- ハードウェア前に代替案の仮想評価を可能にする
-
シーソーバランス手法が柔軟性を提供
- 複数の配分戦略が可能
- ビジネス制約(コスト、流用、タイミング)に基づく最適化が可能
- トレードオフを明示的かつ定量化可能にする
-
検証戦略は配分と整合が必要
- HARDPOINTレベルでテストしてサブシステム適合を証明
- 統合テストがインターフェース仮定を検証
- 車両からコンポーネントレベまでのトレーサビリティ
9.2 他システムへの適用
このHARDPOINTベースのカスケーディング手法は以下にも適用可能:
- 衝突安全: エネルギー吸収配分(前部構造 / 側部構造 / 拘束システム)
- 熱マネジメント: 放熱配分(ラジエータ / エアフロー / 冷却システム)
- 燃費: 損失配分(エンジン / トランスミッション / タイヤ転がり抵抗 / 空力)
- 乗り心地: 入力絶縁配分(タイヤ / サスペンション / ボディ構造 / シート)
9.3 将来の方向性
-
AI/ML統合
- 過去データから最適なシーソーバランスを学習する機械学習
- 自動化されたCAEモデル相関と更新
-
リアルタイムコラボレーション
- 分散チーム向けクラウドベースRecurDynシミュレーション
- 継続的なHARDPOINTモニタリングのためのデジタルツイン
-
モデルベースシステムズエンジニアリング(MBSE)
- 要件カスケードのSysMLモデリング
- 自動化されたトレーサビリティと変更影響解析
-
不確実性定量化
- 製造ばらつきを考慮した確率的配分
- HARDPOINTでのロバスト設計最適化
付録A:用語集
| 用語 | 定義 |
|---|---|
| HARDPOINT | サブシステム間の境界を定義する物理的なインターフェース・取付点 |
| RecurDyn | 車両シミュレーション用マルチボディダイナミクスCAEソフトウェア |
| シーソーバランス | 支点コンセプトを用いて2つのサブシステム間で要件を配分する手法 |
| 伝達関数 | 周波数領域での入力加振に対する出力応答の比 |
| 寄与度解析 | 全体応答をサブシステム寄与に分離するCAE技術 |
| 2次成分 | エンジン回転周波数の2倍の振動周波数成分 |
| 伝達率 | 入力振動に対する伝達振動の比 |
付録B:RecurDynモデル設定例
B.1 パワープラント剛体特性
エンジンブロック:
- 質量: 145 kg
- Ixx: 8.5 kg·m²
- Iyy: 6.2 kg·m²
- Izz: 9.1 kg·m²
- 重心位置: クランク中心線から(X=0, Y=0, Z=50) mm
B.2 マウントブッシュ剛性マトリクス(マウント#1)
6自由度剛性 [N/mm または Nm/deg]:
Kx Ky Kz Krx Kry Krz
X [ 180 0 0 0 0 0 ]
Y [ 0 120 0 0 0 0 ]
Z [ 0 0 350 0 0 0 ]
Rx[ 0 0 0 500 0 0 ]
Ry[ 0 0 0 0 500 0 ]
Rz[ 0 0 0 0 0 500 ]
B.3 加振力定義
燃焼力(クランクシャフトに作用):
- 基本次数: 800 RPM = 13.33 Hz
- 2次成分: 26.67 Hz、振幅 = 850 N
- 4次成分: 53.33 Hz、振幅 = 320 N
- 位相関係: 点火順序に基づく(1-3-4-2)
付録C:参考文献
- ISO 2631-1:1997, 「機械的振動及び衝撃 – 全身振動への人体ばく露の評価」
- SAE J1470, 「車両ダイナミクス用語」
- RecurDynユーザーマニュアル, Function Bay Inc.
- “Vehicle Noise and Vibration Refinement,” Xu Wang et al., Woodhead Publishing
- “Automotive Engineering Fundamentals,” Richard Stone, SAE International
ドキュメント情報
- 作成日: 2026-01-18
- バージョン: 1.0
- 作成者: Claude (Anthropic)
- 目的: 自動車V&V開発プロセスの技術ガイダンス
- 対象読者: システムエンジニア、NVHエンジニア、CAE解析者
本ドキュメントは、HARDPOINTメソドロジーとCAEシミュレーションツールを用いた自動車要件カスケーディングの数値ベースアプローチを示しています。シーソーバランスコンセプトは、明確なインターフェース定義と検証戦略を維持しながら、車両レベル要件をサブシステムレベルに配分するための柔軟なフレームワークを提供します。
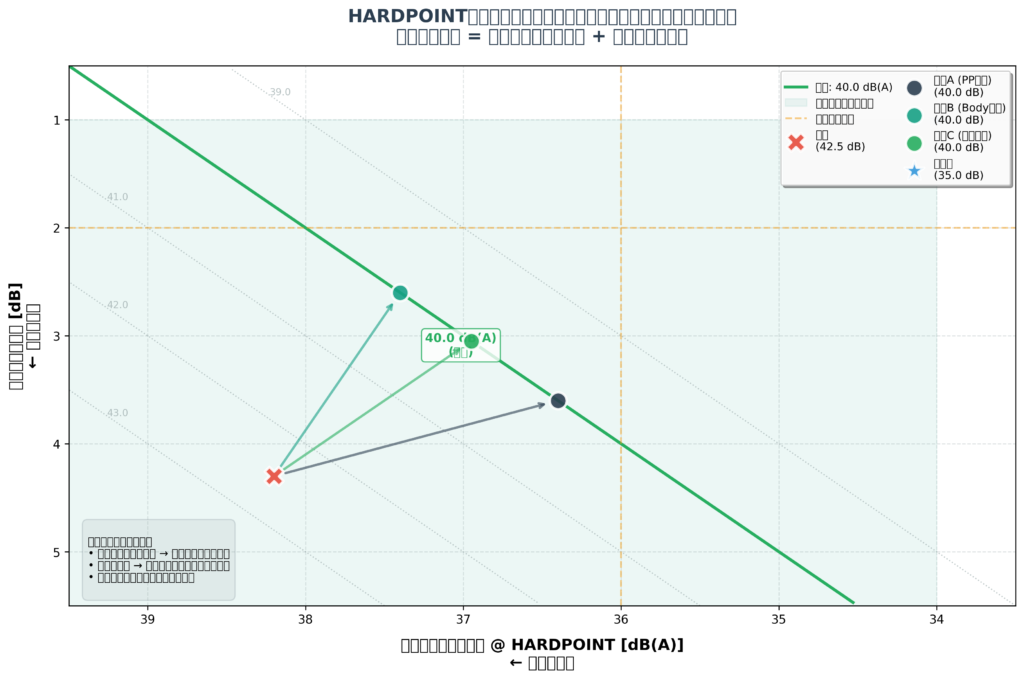
HARDPOINT Cascading Scatter Plot 実装計画
1. グラフの構成要素
軸定義
-
X軸 (Powerplant Performance): HARDPOINTでのパワープラント加振レベル [dB(A)]
- 範囲例: 34.0 – 40.0 dB(A)
- 低い値 = 優れた性能(静かなエンジン)
-
Y軸 (Body Performance): ボディ増幅係数 [dB]
- 範囲例: +1.0 – +6.0 dB
- 低い値 = 優れた性能(低伝達率)
データポイント
-
現状点(ベースライン)
- Powerplant: 38.2 dB(A)
- Body: +4.3 dB
- Vehicle: 42.5 dB(A)
- 色: 赤(目標未達成)
-
目標達成点(複数の戦略)
-
戦略A (Powerplant重視 70/30):
- PP: 36.4 dB(A), Body: +3.6 dB → Vehicle: 40.0 dB(A)
-
戦略B (Body重視 30/70):
- PP: 37.4 dB(A), Body: +2.6 dB → Vehicle: 40.0 dB(A)
-
戦略C (バランス 50/50):
- PP: 36.95 dB(A), Body: +3.05 dB → Vehicle: 40.0 dB(A)
-
色: 緑(目標達成)
-
-
理想点(技術的限界)
- PP: 34.0 dB(A), Body: +1.0 dB → Vehicle: 35.0 dB(A)
- 色: 青(ベストケース)
等値線(Iso-performance Lines)
車両全体性能が同じになる組み合わせを線で表示:
- Vehicle = 40.0 dB(A) (目標線)- 太線、緑
- Vehicle = 41.0 dB(A) – 点線
- Vehicle = 42.0 dB(A) – 点線
- Vehicle = 43.0 dB(A) – 点線
数式:
Vehicle_dB = Powerplant_dB + Body_Amplification_dB
Y = Target - X
例: 40.0 dB(A)目標線
- X=36.0 → Y=+4.0
- X=37.0 → Y=+3.0
- X=38.0 → Y=+2.0
- X=39.0 → Y=+1.0
実現可能領域(Feasible Region)
-
技術的制約:
- PP下限: 34.0 dB(A)(技術限界)
- Body下限: +1.0 dB(完全遮音は不可能)
-
コスト制約:
- PP: 36.0以下 = 高コスト(バランスシャフト等)
- Body: +2.0以下 = 高コスト(大量制振材)
-
実現可能ゾーン: 半透明の緑色エリア
改善ベクトル
現状点から各戦略への矢印:
- ベースライン → 戦略A(PP重視): 水平方向に長い矢印
- ベースライン → 戦略B(Body重視): 垂直方向に長い矢印
- ベースライン → 戦略C(バランス): 対角線矢印
2. 実装方法
オプションA: PowerPoint直接作成(PptxGenJS)
- メリット: 既存プレゼンに統合しやすい
- 制約: 散布図の柔軟性が限定的、等値線の描画が複雑
- 実装: PptxGenJS の SCATTER チャートを使用
オプションB: Python + Matplotlib → 画像 → PowerPoint
- メリット: 高度なカスタマイズ可能、等値線・注釈が自由
- 実装手順:
- Python/Matplotlibで散布図作成
- PNG/JPG画像として保存
- PptxGenJSで画像を新スライドに挿入
オプションC: Excel チャート → PowerPoint
- メリット: データ編集が容易
- 制約: 等値線の自動描画が困難
推奨: オプションB(Python + Matplotlib)
- 最も柔軟性が高い
- 等値線、注釈、カスタムスタイリングが容易
- 高品質な図が作成可能
3. Python実装の詳細設計
データ構造
# 戦略ポイント
strategies = {
'baseline': {'pp': 38.2, 'body': 4.3, 'vehicle': 42.5, 'color': '#E74C3C', 'label': '現状'},
'strategy_a': {'pp': 36.4, 'body': 3.6, 'vehicle': 40.0, 'color': '#2C3E50', 'label': '戦略A (PP重視)'},
'strategy_b': {'pp': 37.4, 'body': 2.6, 'vehicle': 40.0, 'color': '#16A085', 'label': '戦略B (Body重視)'},
'strategy_c': {'pp': 36.95, 'body': 3.05, 'vehicle': 40.0, 'color': '#27AE60', 'label': '戦略C (バランス)'},
'ideal': {'pp': 34.0, 'body': 1.0, 'vehicle': 35.0, 'color': '#3498DB', 'label': '理想点'}
}
# 等値線用のターゲット値
iso_lines = [39.0, 40.0, 41.0, 42.0, 43.0] # dB(A)
グラフ要素
- 背景グリッド: 軽いグレー
- 軸ラベル:
- X: “パワープラント性能 @ HARDPOINT [dB(A)]”
- Y: “ボディ増幅係数 [dB]”
- タイトル: “HARDPOINTカスケーディング:シーソーバランストレードオフ”
- 凡例: 右上に配置
- 注釈:
- 目標線に “目標: 40.0 dB(A)” ラベル
- 実現可能領域に “技術的実現可能ゾーン” テキスト
- 矢印: ベースラインから各戦略への改善パス
スタイリング
-
カラーパレット: 既存プレゼンと統一
- Primary: #16A085
- Secondary: #2C3E50
- Accent: #F39C12
- Red: #E74C3C
- Green: #27AE60
- Blue: #3498DB
-
フォント: Arial(PowerPointと同じ)
-
マーカーサイズ: 大きめ(150-200)で視認性確保
-
線の太さ: 目標線=2.5pt、その他=1.0pt
4. 実装ステップ
Phase 1: Pythonスクリプト作成
- ✓ 必要なライブラリ導入(matplotlib, numpy)
- ✓ データポイント定義
- ✓ 等値線計算関数
- ✓ 散布図プロット
- ✓ 等値線追加
- ✓ 実現可能領域の塗りつぶし
- ✓ 矢印(改善ベクトル)追加
- ✓ 注釈・ラベル追加
- ✓ 画像保存(高解像度PNG、300dpi)
Phase 2: PowerPointスライド追加
- ✓ 既存プレゼンテーションを読み込み
- ✓ 新しいスライドを追加
- ✓ タイトル設定
- ✓ 生成した散布図画像を挿入
- ✓ 説明テキスト追加
- ✓ 保存
Phase 3: 検証
- ✓ 視覚的な確認(画像品質、読みやすさ)
- ✓ データポイントの正確性確認
- ✓ 等値線の計算確認
- ✓ PowerPointでの表示確認
5. 期待される成果物
主要な図
“hardpoint_cascading_scatter.png”
- サイズ: 1920x1080px(16:9、300dpi)
- 形式: PNG(透明背景なし、白背景)
PowerPointスライド
既存プレゼンに追加される新スライド:
- タイトル: “HARDPOINTカスケーディング分析”
- サブタイトル: “シーソーバランストレードオフの可視化”
- 左側(60%幅): 散布図画像
- 右側(40%幅): キーインサイト
- 複数の達成経路が存在
- トレードオフの定量化
- 最適バランスの選択基準
6. 拡張アイデア
追加要素(オプション)
- コスト等値線: 同じ開発コストになる組み合わせ
- 開発期間等値線: 同じ開発時間の組み合わせ
- リスク評価: ポイントの大きさでリスクレベルを表現
- 感度分析: 小さな変動の影響をエラーバーで表示
- 3次元表示: Z軸にコストや開発期間を追加
インタラクティブ版(将来)
- Plotlyを使用したインタラクティブHTMLグラフ
- ホバーで詳細データ表示
- ズーム・パン機能
7. 実装時の注意点
データの正確性
- 実際のCAE結果から数値を取得
- 加算則の確認(dBは対数なので単純加算でOK)
- 物理的に矛盾がないか検証
視覚的明瞭性
- 軸の範囲を適切に設定(データが中央に配置されるように)
- ラベルの重複を避ける
- 色のコントラストを確保(アクセシビリティ)
プレゼンテーションとの統合
- 既存スライドのデザインと調和
- フォント・色を統一
- 適切な位置に挿入(スライド7の後など)
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
HARDPOINT Cascading Scatter Plot
シーソーバランストレードオフの可視化
"""
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import numpy as np
from matplotlib import rcParams
# 日本語フォント設定(環境に応じて調整)
rcParams['font.family'] = 'sans-serif'
rcParams['font.sans-serif'] = ['Arial', 'DejaVu Sans']
# カラーパレット(プレゼンテーションと統一)
colors = {
'primary': '#16A085',
'secondary': '#2C3E50',
'accent': '#F39C12',
'red': '#E74C3C',
'green': '#27AE60',
'blue': '#3498DB',
'muted': '#95A5A6'
}
# データポイント定義
strategies = {
'baseline': {
'pp': 38.2,
'body': 4.3,
'vehicle': 42.5,
'color': colors['red'],
'label': '現状\n(42.5 dB)',
'marker': 'X',
'size': 250
},
'strategy_a': {
'pp': 36.4,
'body': 3.6,
'vehicle': 40.0,
'color': colors['secondary'],
'label': '戦略A (PP重視)\n(40.0 dB)',
'marker': 'o',
'size': 200
},
'strategy_b': {
'pp': 37.4,
'body': 2.6,
'vehicle': 40.0,
'color': colors['primary'],
'label': '戦略B (Body重視)\n(40.0 dB)',
'marker': 'o',
'size': 200
},
'strategy_c': {
'pp': 36.95,
'body': 3.05,
'vehicle': 40.0,
'color': colors['green'],
'label': '戦略C (バランス)\n(40.0 dB)',
'marker': 'o',
'size': 200
},
'ideal': {
'pp': 34.0,
'body': 1.0,
'vehicle': 35.0,
'color': colors['blue'],
'label': '理想点\n(35.0 dB)',
'marker': '*',
'size': 300
}
}
# 図の作成
fig, ax = plt.subplots(figsize=(12, 8), facecolor='white')
# 軸の範囲設定
x_min, x_max = 33.5, 39.5
y_min, y_max = 0.5, 5.5
ax.set_xlim(x_min, x_max)
ax.set_ylim(y_min, y_max)
# グリッド
ax.grid(True, linestyle='--', alpha=0.3, color=colors['muted'])
# 等値線(車両性能が同じになる組み合わせ)
iso_values = [39.0, 40.0, 41.0, 42.0, 43.0]
x_iso = np.linspace(x_min, x_max, 100)
for iso_val in iso_values:
y_iso = iso_val - x_iso
# Y軸範囲内のみプロット
mask = (y_iso >= y_min) & (y_iso <= y_max)
if iso_val == 40.0:
# 目標線は太く、緑色
ax.plot(x_iso[mask], y_iso[mask],
color=colors['green'], linewidth=2.5, linestyle='-',
label=f'目標: {iso_val} dB(A)', zorder=2)
# ラベル追加
if np.any(mask):
idx = len(x_iso[mask]) // 2
ax.text(x_iso[mask][idx], y_iso[mask][idx] + 0.2,
f'{iso_val} dB(A)\n(目標)',
color=colors['green'], fontsize=10, fontweight='bold',
ha='center', bbox=dict(boxstyle='round,pad=0.3',
facecolor='white', edgecolor=colors['green'], alpha=0.8))
else:
# その他の等値線
ax.plot(x_iso[mask], y_iso[mask],
color=colors['muted'], linewidth=1.0, linestyle=':',
alpha=0.6, zorder=1)
# ラベル(右端に小さく)
if np.any(mask):
idx = -5
ax.text(x_iso[mask][idx], y_iso[mask][idx],
f'{iso_val}',
color=colors['muted'], fontsize=8, alpha=0.7)
# 実現可能領域の塗りつぶし(技術的限界内)
# PP技術限界: 34.0 dB(A), Body技術限界: +1.0 dB
feasible_x = [34.0, 39.5, 39.5, 34.0]
feasible_y = [1.0, 1.0, 5.5, 5.5]
ax.fill(feasible_x, feasible_y, color=colors['primary'], alpha=0.08,
label='技術的実現可能領域', zorder=0)
# 高コストゾーンの境界線(PP < 36.0 または Body < 2.0)
ax.axvline(x=36.0, color=colors['accent'], linestyle='--',
linewidth=1.5, alpha=0.5, label='高コスト境界')
ax.axhline(y=2.0, color=colors['accent'], linestyle='--',
linewidth=1.5, alpha=0.5)
# データポイントをプロット
for key, data in strategies.items():
ax.scatter(data['pp'], data['body'],
c=data['color'], marker=data['marker'],
s=data['size'], edgecolors='white', linewidths=2,
label=data['label'], zorder=5, alpha=0.9)
# 改善ベクトル(矢印)
baseline = strategies['baseline']
for key in ['strategy_a', 'strategy_b', 'strategy_c']:
target = strategies[key]
ax.annotate('', xy=(target['pp'], target['body']),
xytext=(baseline['pp'], baseline['body']),
arrowprops=dict(arrowstyle='->', lw=2, color=target['color'],
alpha=0.6, shrinkA=10, shrinkB=10),
zorder=3)
# 軸ラベル
ax.set_xlabel('パワープラント性能 @ HARDPOINT [dB(A)]\n← 優れている',
fontsize=13, fontweight='bold', labelpad=10)
ax.set_ylabel('ボディ増幅係数 [dB]\n← 優れている',
fontsize=13, fontweight='bold', labelpad=10)
# タイトル
ax.set_title('HARDPOINTカスケーディング分析:シーソーバランストレードオフ\n車両全体性能 = パワープラント性能 + ボディ増幅係数',
fontsize=15, fontweight='bold', pad=20, color=colors['secondary'])
# X軸を反転(左に行くほど優れている)
ax.invert_xaxis()
# Y軸を反転(下に行くほど優れている)
ax.invert_yaxis()
# 凡例(2列で表示)
legend = ax.legend(loc='upper right', fontsize=9, frameon=True,
shadow=True, ncol=2, columnspacing=1.0)
legend.get_frame().set_facecolor('white')
legend.get_frame().set_alpha(0.95)
# 注釈テキスト(左下)
annotation_text = """
トレードオフの原則:
• パワープラント改善 → ボディ要件緩和可能
• ボディ改善 → パワープラント要件緩和可能
• 複数の経路で同じ目標を達成可能
"""
ax.text(0.02, 0.02, annotation_text, transform=ax.transAxes,
fontsize=9, verticalalignment='bottom',
bbox=dict(boxstyle='round,pad=0.5', facecolor=colors['muted'],
alpha=0.15, edgecolor=colors['secondary']))
# レイアウト調整
plt.tight_layout()
# 画像保存(高解像度)
output_path = 'hardpoint_cascading_scatter.png'
plt.savefig(output_path, dpi=300, bbox_inches='tight', facecolor='white')
print(f"✓ 散布図を保存しました: {output_path}")
# 表示(オプション)
# plt.show()
plt.close()
Claude Cowork 2026/1/18

